※この記事は自分の学習と効率化のために、ChatGPTに書いてもらったものをベースとしています。
画像と赤文字で記載されている箇所などは私のコメントや感想部分です。
3.確率とフィギュア・サブプロット
確率の基本概念と公理の紹介
確率は、事象が起こる可能性や不確実性を数値化するための道具です。確率の基本的な定義は以下の通りです。
1. 試行 (Trial): 結果が偶然に左右される行為や観察。
2. 事象 (Event): 試行において考慮される結果や結果の集合。
確率の公理は、確率に関する基本的な性質やルールを定めたもので、以下の3つの公理があります。
1. 任意の事象 \( A \) に対して、\( 0 \leq P(A) \leq 1 \)
2. 標本空間 \( S \) に対して、\( P(S) = 1 \)
3. 互いに排反な事象の列 \( A_1, A_2, … \) に対して、\[ P(A_1 \cup A_2 \cup …) = P(A_1) + P(A_2) + … \]
文系の私にはちんぷんかんぷんですが、確率の3公理を調べたら
1.確率は0以上1以下である
2.全事象は1である
3.各事象を足したら1になる(サイコロのすべての確率を足したら1)
といった、普通のことを数学的に難しくいってるだけですね
条件付き確率とベイズの定理の説明
条件付き確率: ある事象 \( B \) が与えられたときの事象 \( A \) の確率。数式で表すと \( P(A|B) \) です。計算方法は以下の通り。
\[ P(A|B) = \frac{P(A \cap B)}{P(B)} \]
ベイズの定理: 条件付き確率を使って、事前の知識や情報を基にした後の事象の確率を更新する方法。数式で表すと:
\[ P(A|B) = \frac{P(B|A) \times P(A)}{P(B)} \]
ここで、
– \( P(A|B) \) は事後確率
– \( P(B|A) \) は尤度
– \( P(A) \) は事前確率
– \( P(B) \) は周辺尤度
条件付き確率は例えばトランプでハートの場合(B)絵札である(A)確率(1/4)といったことで、
ベイズの定理はもっとややこしいですね。一応調べた感じだと、
(A)引いたカードがハート
(B)引いたカードが絵札
すべてのカードが52枚、ハートは13枚、絵札は12枚、ハートの絵札は3枚なので
事後確率は絵札を引いた後にそれがハートである確率(1/4)
尤度はハートのカードが絵札である確率(3/13)
事前確率はカードがハートである確率(1/4)
周辺尤度はカードが絵札である確率(31/3)
ということです。それぞれをベイズの定理に当てはめると事後確率が導けるということみたいですね
複数の確率分布を一つのフィギュア内に表示する方法
matplotlibのサブプロットを使用して、複数の確率分布を一つのフィギュア内に表示する方法を紹介します。
import numpy as np
import matplotlib.pyplot as plt
# データの生成
x = np.linspace(-10, 10, 400)
y1 = (1 / np.sqrt(2 * np.pi)) * np.exp(-0.5 * x**2) # 正規分布
y2 = np.exp(-abs(x)) / 2 # ラプラス分布
# フィギュアとサブプロットの生成
fig, axs = plt.subplots(2, 1, figsize=(8, 6))
# 正規分布のプロット
axs[0].plot(x, y1, label="Normal Distribution")
axs[0].set_title("Normal Distribution")
axs[0].legend()
# ラプラス分布のプロット
axs[1].plot(x, y2, color='red', label="Laplace Distribution")
axs[1].set_title("Laplace Distribution")
axs[1].legend()
# レイアウトの調整
plt.tight_layout()
plt.show()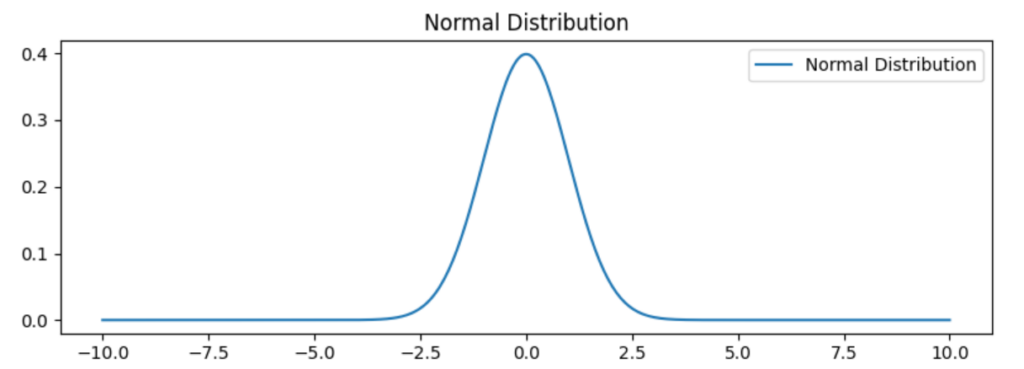
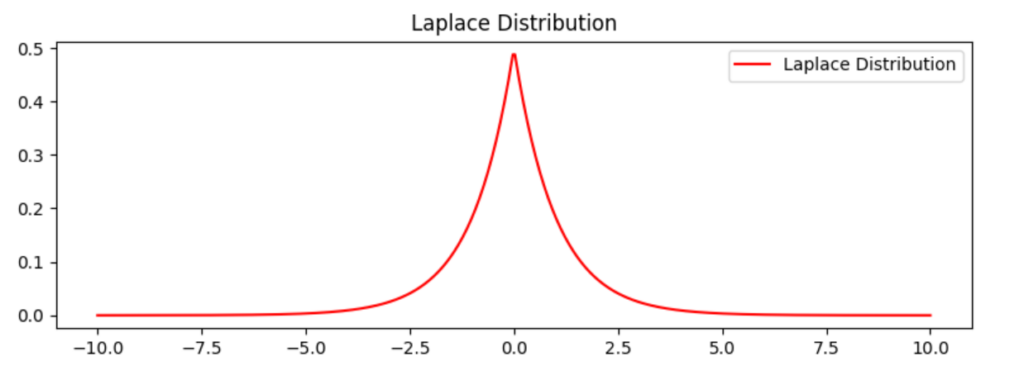
上記のコードでは、正規分布とラプラス分布の2つの確率分布を縦に2つのサブプロットで一つのフィギュア内に表示しています。
以上で、確率の基本概念と公理、条件付き確率とベイズの定理、そしてmatplotlibを使用しての複数の確率分布の可視化方法について学びました。




