※この記事は自分の学習と効率化のために、ChatGPTに書いてもらったものをベースとしています。
画像と赤文字で記載されている箇所などは私のコメントや感想部分です。
2.記述統計と基本的なプロットの作成
平均、中央値、モードの計算
記述統計の最も基本的な計算として、データの中心傾向を示す平均、中央値、モードの計算があります。
平均 (mean): データの合計をデータの個数で割ったものです。
中央値 (median): データを小さい順に並べたときに中央に位置する値です。
モード (mode): データの中で最も頻繁に現れる値です。
Pythonのstatistics: ライブラリを使えばこれらを簡単に計算できます。
import statistics
data = [1, 2, 3, 4, 2, 3, 3, 5, 6]
mean = statistics.mean(data)
median = statistics.median(data)
mode = statistics.mode(data)
print(f"Mean: {mean}, Median: {median}, Mode: {mode}")
# Mean: 3.2222222222222223, Median: 3, Mode: 3折れ線グラフや散布図を用いたデータの可視化
データの傾向や関係を直感的に理解するためには、可視化が非常に役立ちます。
1. 折れ線グラフ: データの変動や時間経過によるトレンドを表示するのに適しています。
2. 散布図: 2つの変数間の関係性を表示するのに適しています。
以下は、matplotlibのpyplot: を使用した基本的なプロット方法です。
import matplotlib.pyplot as plt
# データの用意
x = [1, 2, 3, 4, 5]
y = [2, 4, 5, 4, 5]
# 折れ線グラフの描画
plt.plot(x, y, label='Line Plot')
# 散布図の描画
plt.scatter(x, y, color='red', label='Scatter Plot')
plt.title('Line and Scatter Plot')
plt.xlabel("X-axis")
plt.ylabel("Y-axis")
plt.legend()
plt.show()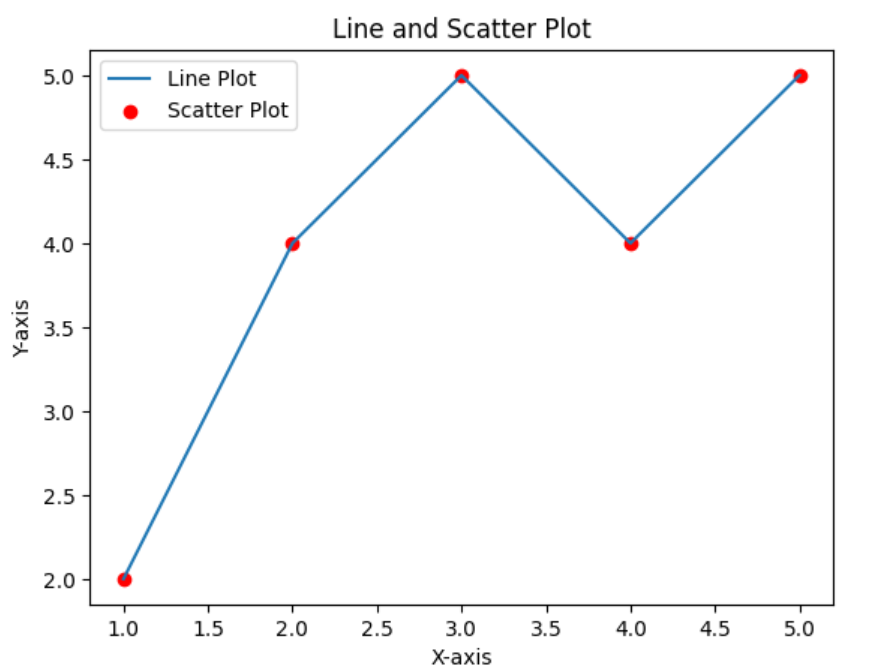
分散、標準偏差、四分位範囲の計算
データのばらつきや分散を評価するための基本的な指標として、以下のものがあります。
分散 (variance): データの各値が平均からどれだけずれているかの平均値。
標準偏差 (standard deviation): 分散の平方根。データのばらつきを数値化したもの。
四分位範囲 (IQR: InterQuartile Range): 第三四分位数と第一四分位数の差。データの中央部の広がりを示す。
variance = statistics.variance(data)
std_dev = statistics.stdev(data)
q1 = statistics.quantiles(data, n=4)[0]
q3 = statistics.quantiles(data, n=4)[2]
iqr = q3 - q1
print(f"Variance: {variance}, Std Dev: {std_dev}, IQR: {iqr}")
# Variance: 2.4444444444444446, Std Dev: 1.5634719199411433, IQR: 2.5ヒストグラムの作成とデータの形状の解釈
ヒストグラムは、データの分布や形状を可視化するのに非常に役立つツールです。
plt.hist(data, bins=10, edgecolor="black")
plt.title("Histogram")
plt.xlabel("Value")
plt.ylabel("Frequency")
plt.show()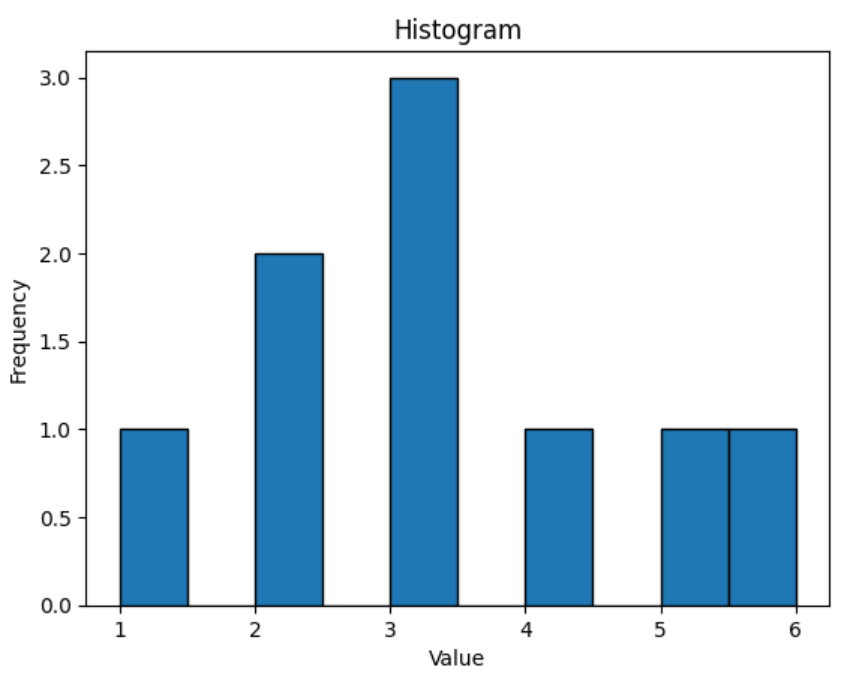
ヒストグラムを観察することで、データの形状(例: 正規分布、左に偏った分布、右に偏った分布など)や、外れ値の存在などの情報を得ることができます。




